|
|
准备分享一些干货了,先写个因子投资系列的吧!因子投资目前是市场上做量化投资最主流的方法论,具体就是基于交易标的的量价信息和其他(包括基本面)信息找到和未来收益率相关的因素。
举个简单的因子:动量因子(20个交易日收益率之和)。如果说动量效应在A股成立的话,那么因子值越大(过去涨幅越大),未来股票上涨的概率就越大。(如下图)
这个概率怎么体现呢,如果只看一只股票,那只能从时序上来判断,回看历史每个交易日的因子值,再对比一下滞后N期的收益情况。如此一来,样本量就太少了,不能说明问题,所以我们把所有的股票拿出来分析一下是不是都存在这样的规律。
怎么判断这个因子是不是有效的呢?最简单直接的方法是看因子和未来收益的相关系数。我们先来看看截面的情况,比如今天是1月3日,我计算好了每只股票的动量因子值(20个交易日收益率之和),如果A股市场存在显著的动量效应,那么因子值越大的股票,未来更趋于上涨,对因子值和未来5日收益率这两个数据求相关系数corr的话,corr应该大于0,并且动量效应越明显,相关系数应该越大。不过这个时候我们看的是某一天,如果这一天计算的横截面的相关系数很大,比如0.05,那可以说在这一天,A股动量效应明显,资金流入到过去涨幅较大的股票里去了,比如前段时间的西安饮食。
问题是,市场一直在变化的,也许昨天是动量效应,今天变成了反转效应怎么办,那也就是说,过去涨的最猛的股票今天就会跌的最惨!那这个动量因子还有没有用?怎么评判因子的有效与否呢?
那我们就要从时间序列上看一下了,如果过去100天,有60天的相关系数为正,30天为负,还有10天为零,那么通过这个因子,我就可以在这100天里,60天挣钱,30天亏钱,10天不亏不挣。不过这里面还有一个问题,如果挣钱的60天是前60天,亏钱的30天是后30天,这个因子你还敢接着用吗?连亏30天是绝大多数人都承受不了的。
所以我们用一张因子的累积IC的图来看因子的表现是不是稳定朝向一个方向的,就是把每天计算的界面相关系数进行累加,如果因子表现比较稳定并且朝着一个方向,IC的图应该是这个样的:
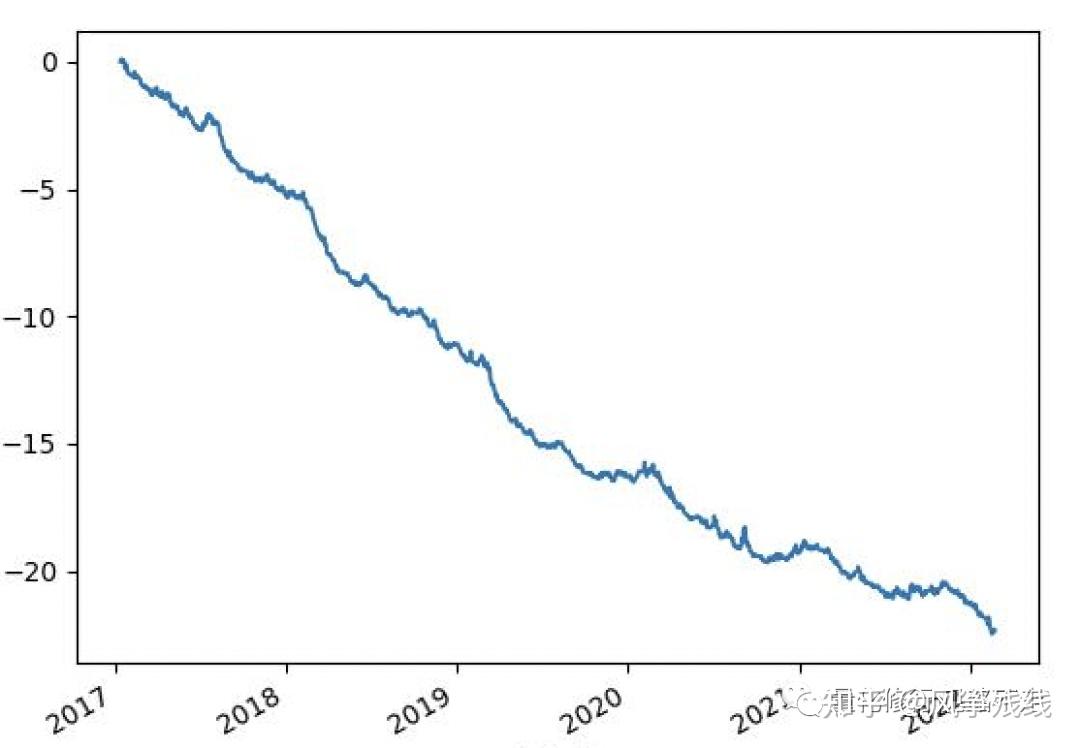
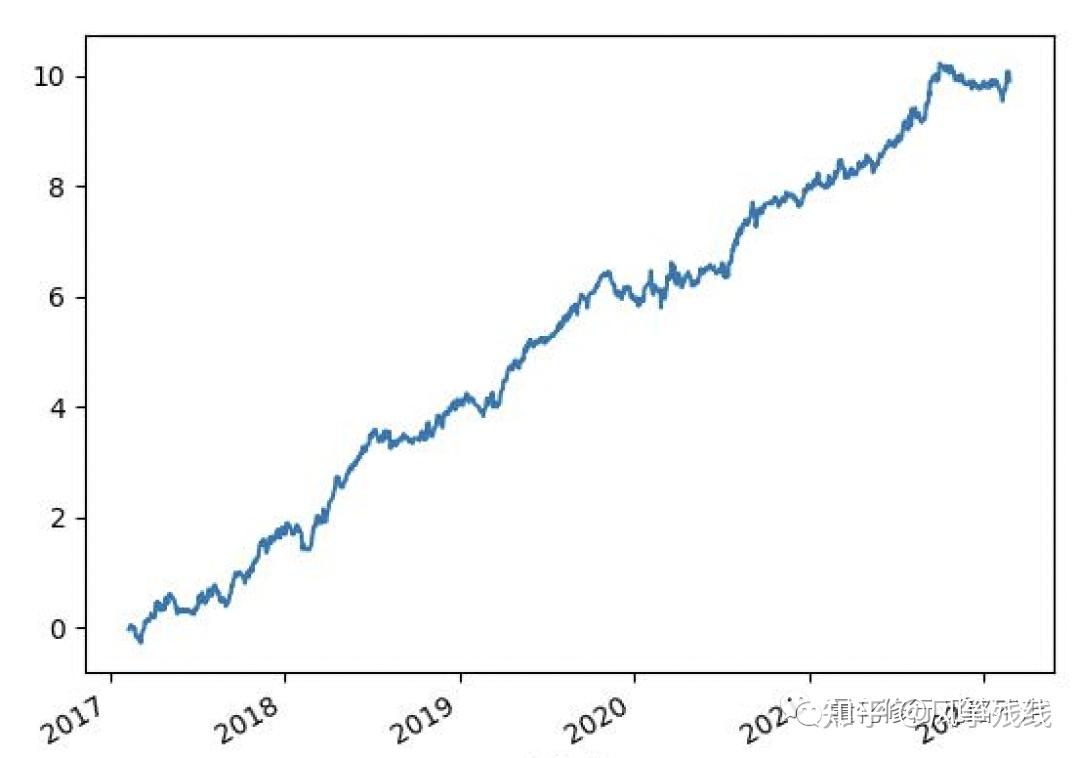
如果是因子表现很不稳定,那应该是这样的:
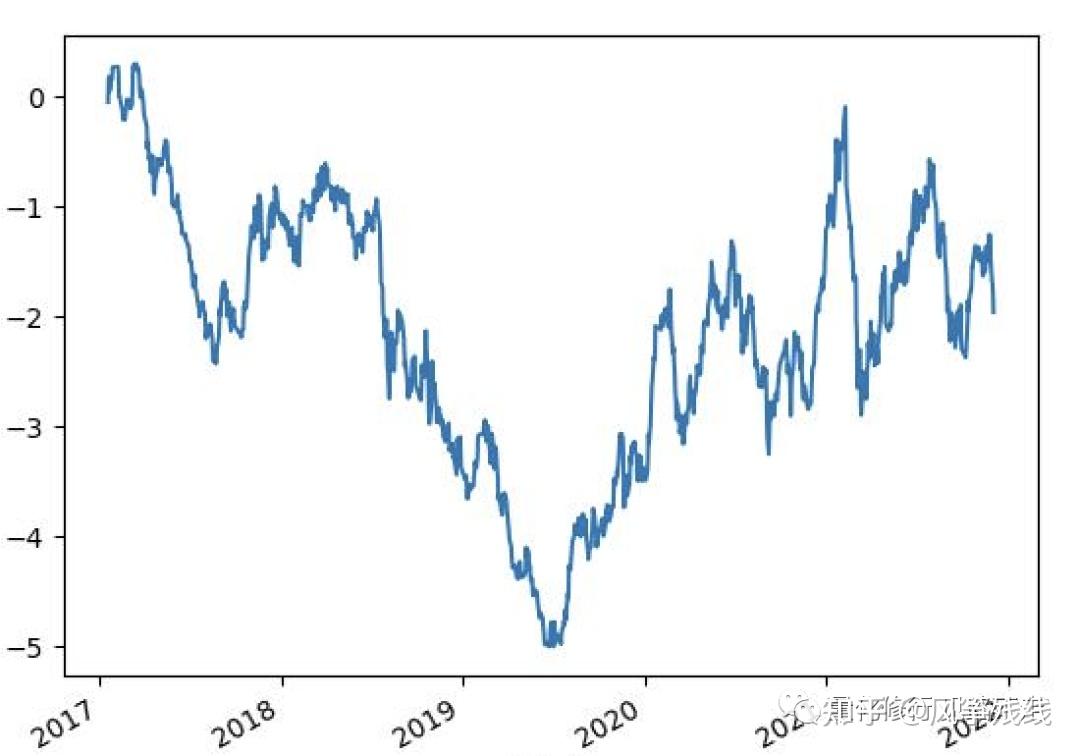
接下来就是用代码实现一下啦:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sympy import subsets
import scipy
import multiprocessing as mp
import os
import warnings
warnings.filterwarnings("ignore")
def y_prepare(df):
df.sort_values([ "ukey","DataDate",],inplace=True)
g = df.groupby('ukey')
df_list = []
for _ , ukeydf in g:
ukeydf['return_one_day'] = ukeydf['Open'].shift(-2) / ukeydf['Open'].shift(-1) -1
ukeydf['return_two_day_close'] = ukeydf['Close'].shift(-2) / ukeydf['Open'].shift(-1) - 1
ukeydf['return_three_day'] = ukeydf['Open'].shift(-3) / ukeydf['Open'].shift(-1) - 1
ukeydf['return_five_day'] = ukeydf['Open'].shift(-6) / ukeydf['Open'].shift(-1) - 1
ukeydf['return_20_day'] = ukeydf['Open'].shift(-21) / ukeydf['Open'].shift(-1) - 1
df_list.append(ukeydf[['ukey','DataDate','return_one_day','return_two_day_close','return_three_day','return_five_day','return_20_day']])
df = pd.concat(df_list,axis=0)
return df
def x_prepare(df, stockdf,):
maxv = df.x.quantile(0.99)
minv = df.x.quantile(0.01)
minv = 0 if minv >= 0 else minv
maxv = 0 if maxv <= 0 else maxv
df[&#34;ukey&#34;] = df[&#34;ukey&#34;].apply(lambda x: int(x[:6]))
factordf = pd.merge(df[[&#39;ukey&#39;,&#39;DataDate&#39;,&#39;x&#39;]],stockdf,on=[&#39;ukey&#39;,&#39;DataDate&#39;],how=&#39;right&#39;)
return factordf
def plot_and_save(df, save_path, save=True, close=False):
ax = df.plot()
fig = ax.get_figure()
if save:
fig.savefig(save_path)
if close:
plt.close(fig)
def run_ic_test(factor_df, ffill=True):
factor_df.sort_values([ &#34;ukey&#34;,&#34;DataDate&#34;,],inplace=True)
g = factor_df.groupby(&#39;ukey&#39;)
if ffill:
factor_df[&#39;x&#39;] = g[&#39;x&#39;].ffill()
factor_df.dropna(subset=&#39;x&#39;, inplace=True)
factor_df = factor_df.fillna(0)
g = factor_df.groupby(&#39;DataDate&#39;)
IC_one_day = []
IC_two_day = []
IC_three_day = []
IC_five_day = []
IC_20_day = []
date_list = []
for _,ukeydf in g:
IC_one_day.append(ukeydf[[&#39;x&#39;,&#39;return_one_day&#39;]].dropna().corr()[&#39;x&#39;][1])
IC_two_day.append(ukeydf[[&#39;x&#39;,&#39;return_two_day_close&#39;]].dropna().corr()[&#39;x&#39;][1])
IC_three_day.append(ukeydf[[&#39;x&#39;,&#39;return_three_day&#39;]].dropna().corr()[&#39;x&#39;][1])
IC_five_day.append(ukeydf[[&#39;x&#39;,&#39;return_five_day&#39;]].dropna().corr()[&#39;x&#39;][1])
IC_20_day.append(ukeydf[[&#39;x&#39;,&#39;return_20_day&#39;]].dropna().corr()[&#39;x&#39;][1])
date_list.append(str(_)[:4])
IC_df = pd.DataFrame(
{&#39;return_one_day&#39;: IC_one_day, &#39;return_two_day_close&#39;: IC_two_day, &#39;return_three_day&#39;: IC_three_day, &#39;return_five_day&#39;: IC_five_day, &#39;return_20_day&#39;: IC_20_day,})
IC_df.index = date_list
for i in IC_df.columns:
IC_df = IC_df.cumsum()
return IC_df
def calculate_IC(name):
factor_name = name
print(name)
factordf = pd.read_csv(rf&#34;./factors/{factor_name.lower()}&#34;, )
factordf[&#39;ukey&#39;] = factordf[&#39;ukey&#39;].astype(str)
factor_df = x_prepare(factordf, stockdf)
IC_df = run_ic_test(factor_df, ffill=False)
for i in IC_df.columns:
plot_and_save(IC_df, rf&#34;{factor_name}_IC_{i}.jpg&#34;, save=True, close=True)
IC_df = run_ic_test(factor_df, ffill=True)
for i in IC_df.columns:
plot_and_save(IC_df, rf&#34;{factor_name}_IC_{i}_fill.jpg&#34;, save=True, close=True)
stockdf = pd.read_csv(&#34;ashareeodprices_total.csv.gz&#34;, )
stockdf = y_prepare(stockdf)
if __name__ == &#34;__main__&#34;:
name_list=[]
path = &#39;./factors&#39;
files = os.listdir(path)
name_list = [x for x in files]
print(&#39;因子个数为:&#39;,len(name_list))
pool = mp.Pool(4)
pool.map(func=calculate_IC, iterable=name_list,chunksize=1)
print(&#34;ty2023new_trade,在后台回复“因子IC测试”即可获得完整数据资源链接!&#34;)这里免费为大家提供2008年以来所有A股的日度行情数据,完整代码以及几个因子例子。
行情数据是这样的:
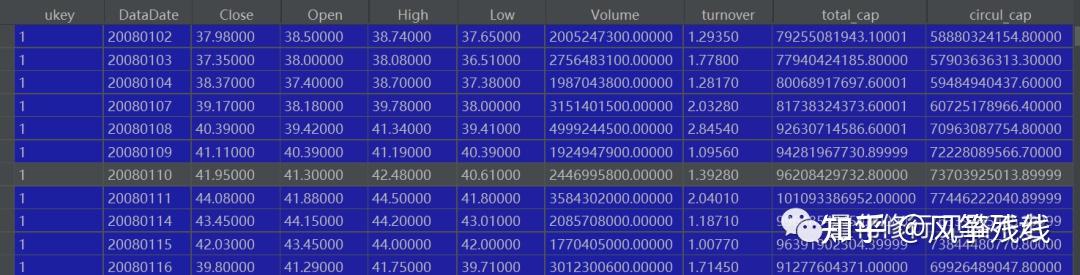
全A行情数据(不复权)
因子数据是这样的:
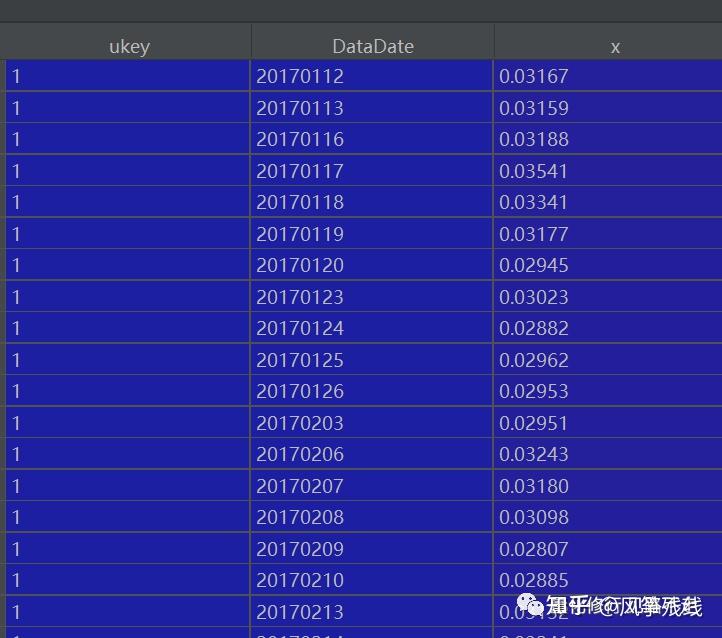
因子数据存储例子
完整代码如下:
大家直接用pycharm或者其他环境下运行evaluater.py即可。fill是补充空缺的值,如果是财务数据的因子,可以保证IC值的连续。
factors里是我随便放入的几个因子。大家也可以把自己写的一些因子放进去(格式要满足上面因子的数据图片就行),可以批量计算出因子值关于未来几日收益率的IC情况了。可以看到自己写的因子在各个历史时间的表现了。
分享不易,转发和点赞是我最大的动力!今天就写到这里吧,过些天再分享一下如何写因子以及构建投资组合。 |
|